シナジェティクスは同時的な論理の首尾一貫性(consistency)を学習や探究に求めない。
より大きなパターンを学ぶ方法は、
過去の首尾一貫性を破壊する新たな経験を生む。
自然界の波動は互いに非同時的に干渉(coherence)することができる。
「コスモグラフィー」カテゴリーアーカイブ
5回対称性の原始シンメトリー
正20面体の対称性のある最密充填のシナジェティクスモデル(右)では
中心の球の半径は、周囲の12個の球の半径よりも小さい。
この5回対称性は紀元前3500年ごろの青銅器時代よりも
2500年以上も先行する海の民による
最古の最密充填モデル(towie stone)で認識されていた。
これは兵器でも装飾でもない、
純粋な幾何学的思考の軌跡にちがいない。
原始シンメトリー感覚は数学と科学を
通底する「構造とパターン」の前駆体である。
SYNERGETICS RBF
5回対称性のある最密充填のシナジェティクスモデル
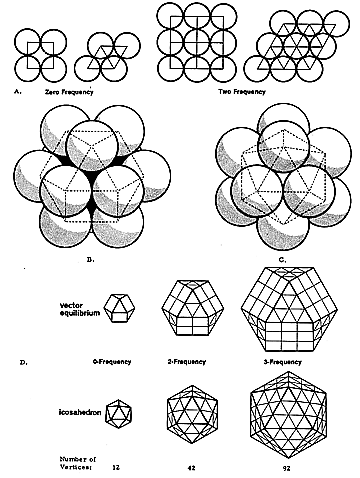
最古の最密充填モデル(towie stone)
スコットランドで出土した約7千年前のtowie stone(最密充填モデル)から
注目すべきは正20面体の対称性をすでに概念化した思考方法にある。
それは顕微鏡がなければ自然界では発見できない方法だ。
観察から発見していないならば
古代ギリシアのプラトン派のモデル言語に圧倒的に先行している。
towie stone

https://www.atlasobscura.com/articles/what-are-scotlands-carved-balls
先験的な構造とパターン
あらゆる構造はテンセグリティである。
隕石で発見されたフラーレーン、深海の放散虫や
動植物の細胞に至るまで。
テンセグリティの美的な構造が生成される過程に
美的な観点が存在しないのは
だれかに発注した構造ではなかったからだ。
真の構造はしっぽのデザイン(tailoring)から生まれない
先験的な構造とパターンだった。
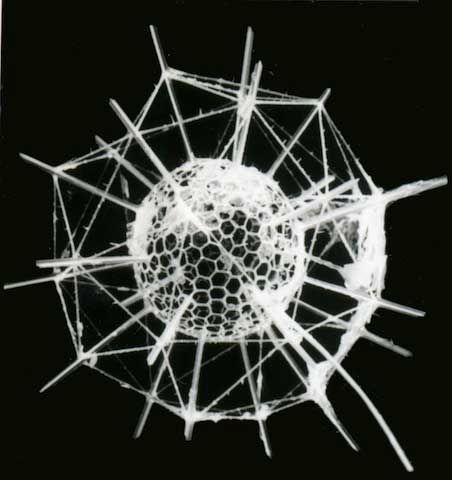
最適な張力・斥力測定方法
張力と圧縮力の見えない相互作用をテンセグリティは視覚化した。
テンセグリティは張力モデルであり、同時に斥力モデルである。
ある特定の張力材による張力を高めると他の2点間距離は増大し
テンセグリティの直径は増大する。
これが原子核モデルの最適な張力と斥力の測定方法である。
SYNERGETICS RBF 1975
Transformation of Six-Strut Tensegrity Structures
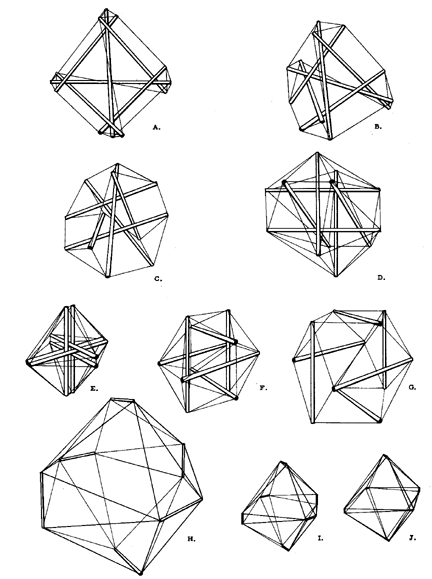
詐欺師
失敗を怖れて要求不満(圧縮力)を高めると
冒険心が失われるばかりか、
自重によって自らを挫折させるノウハウを身につけた詐欺師になる。
圧縮材は、閉じた気体分子でも十分だ。
テンセグリティにおいては圧縮力は自重ではなく張力から生まれる。
原型(prototype)
(1)形態が圧縮材の配置パターンを決める
(2)張力が圧縮力を決める。
(3)張力が圧縮材の細長比を決める。
(4)その細長比が最小限の圧縮材の重量をきめる。
(5)張力材の長さが固有振動数を決める。
(6)ネットワークパターンが構造全体の強度とその共鳴作用をきめる。
構成要素(皮膜材、張力材、圧縮力材、ネットワークパターン)が
相互作用しながらテンセグリティを生成する構造の原型は
どの構成要素からも推測できない。
鋳型とはプロトタイプの異名である。
SYNERGETICS RBF 1975
Tetrahedral module
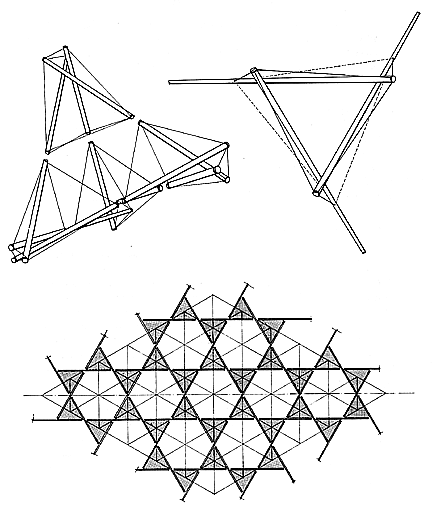
自律のための総三角形化
ジオデシックドームでさえ半球ゆえにまだ総三角形化されていない。
基礎がなければ不安定である。
構造の不安定さは総三角形化の不完全さから生まれる。
この欠如は表面的な改善や対処によって解消することが出来ない。
ジョイントの金属化などの合成化は重量とコストの増加を伴う。
構造への理解はあらゆる関係における自己への働きと
その相互作用への不断の気づきによって総三角形化される。
基礎を不要とする世界初の完全自律型テンセグリティシェルター 直径6.5m 重量30kg

用途開発(utilization)
ジオデシック理論から
シナジェティクスへ飛躍する挑戦に興味がない場合は
構造からシナジェティクスへの接続と同じ
構造とパターンの有用性の変換力に起因するだろう。
原理と工学の相互関係が有用性(とその無限性)を生むプロセスは
シナジェティクスを生成する。
用途開発(utilization)は応用技術ではなく、
先行するこれまでの標準の概念を破壊するテクノロジーである。
真の有用性は包括的な気づきによって発見される美的な解決方法である。
中心核の生成
構造はあらゆる関係における自己(中心核)への働きと
その相互作用への不断の気づきによって総三角形化される。
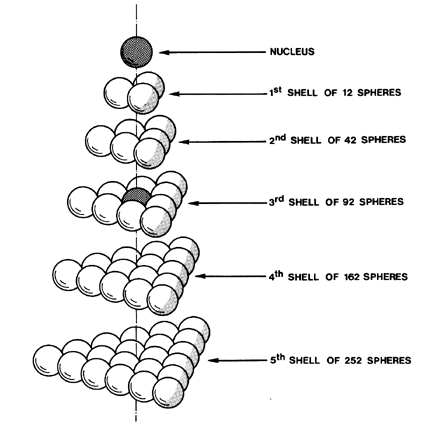
中心核は、周期的な層に生成される。
SYNERGETICS RBF 1975
Fig. 415.55 Tetrahedral Closest Packing of Spheres: Nucleus and Nestable Configurations:

コメントを投稿するにはログインしてください。